Это метод построения моделей классификации данных, основанный на создании композиции (ансамбля) базовых алгоритмов \(b^{x}\).

Каждый базовый алгоритм \(b(x)\) возвращает вещественное значение (обычно это вероятность принадлежности классу). Решающее правило \(С\) возвращает результат классификации.

Корректирующая операция \(F(b_{1}(x),...,b_{T}(x))\) обычно линейна. В простейшем случае это среднее арифметическое или другие модификации среднего (бэггинг, метод случайных подпространств). Но в бустинге применяется взвешенное голосование — строится линейная комбинация базовых алгоритмов, коэффициенты которой \(\alpha_{t}\) подбираются жадным образом.

Вводится функция потерь \(L(a,y)\), минимизируется функционал ошибки \(Q\).

В задачах классификации \(L\) — это функция, зависящая от отступов (которые интерпретируются как степень принадлежности объекта классу), а в задачах регрессии это

Для задач с произвольным числом классов соответствующим образом переопределяются отступы. Рекомендуется использовать простое голосование базовых алгоритмов, так как превосходство различных вариантов со взвешиванием сильно зависит от задачи.

Бэггинг (bagging, bootstrap aggregation)

Базовые алгоритмы обучаются независимо на случайных подвыборках размера исходной выборки с повторениями. Производится контроль минимального качества базовых алгоритмов для включения их в композицию. Ответом является простое усреднение результатов.

Метод случайных подпространств (RSM, Random Subspace Method)

Базовые алгоритмы обучаются независимо на случайных подмножествах признаков. Полезен в случае, когда признаков больше, чем обучающих примеров, или много неинформативных признаков.

Бэггинг и метод случайных подпространств можно применять одновременно.

В процессе обучения алгоритмов добиваются как можно меньшей их коррелированности для уменьшения ошибки.

Эти алгоритмы эффективнее для коротких обучающих выборок, бустинг же лучше для больших выборок и классов с границами сложной формы.

Они эффективно распараллеливаются, в отличие от бустинга, где базовые алгоритмы добавляются последовательно.

Квазилинейная композиция (смесь алгоритмов, Mixture of Experts)

Коэффициенты композиции зависят от x, носят название функций компетентности (а также «шлюз», «gate»). Функции компетентности выбираются исходя из знаний о предметной области. Количество базовых алгоритмов может быть задано заранее или определяться автоматически.

Рассматривается задача бинарной классификации \(b_{t}:X\rightarrow \left \{ -1,+1 \right \}\) (существует модификация с возможностью отказа от классификации \(b_{t}:X\rightarrow \left \{ -1,0,+1 \right \}\)).

Решающее правило: \(C(b)=sign(b)\).

Композиция: \(a(x)=C(F(b_{1}(x),...,b_{T}(x)))=sign\left ( \sum _{t=1}^{T} \alpha _{t}b_{t}(x)\right )\).

Функционал ее ошибки — пороговая функция потерь:

Используют для решения задачи гладкие аппроксимации \(Q\).

В случае AdaBoost это

где

— отступ объекта обучающей выборки.

где \(w_{i}=exp\left ( -y_{i}\sum_{t=1}^{T-1}\alpha_{t}b_{t}(x_{i})\right )\) — веса объектов (большие отрицательные значения отступов соответствуют плохо распознающимся объектам и дают большие значения весов).

Рассматриваются нормированные веса объектов: \(\tilde{w}=w_{i}/\sum_{j=1}^{N}w_{j}\).

Вводится понятие взвешенного числа ошибочных \(N(b;W)\) классификаций:

Доказана теорема, что если

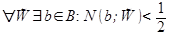
то

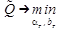
когда

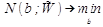
и

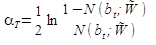
При начале обучения алгоритма веса объектов инициализируются Ǝ:

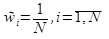
На каждой итерации базовый алгоритм решает задачу

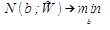
Веса алгоритмов вычисляются по формуле:

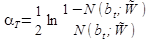
На случай \(N(b_{t};\tilde{W})=0\) используют формулу

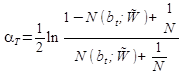
Затем обновляются веса объектов:

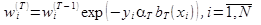
Далее веса объектов заново нормируются и цикл повторяется до достижения заданного количества базовых алгоритмов или до начала роста ошибки на валидационной выборке.