Настройка узла ARIMA
Окно Настройки узла ARIMA включает три вкладки: Выбор колонок (где необходимо выбрать Целевую переменную), Настройки и Общие.
Вкладка Настройки позволяет настроить работу алгоритма узла:
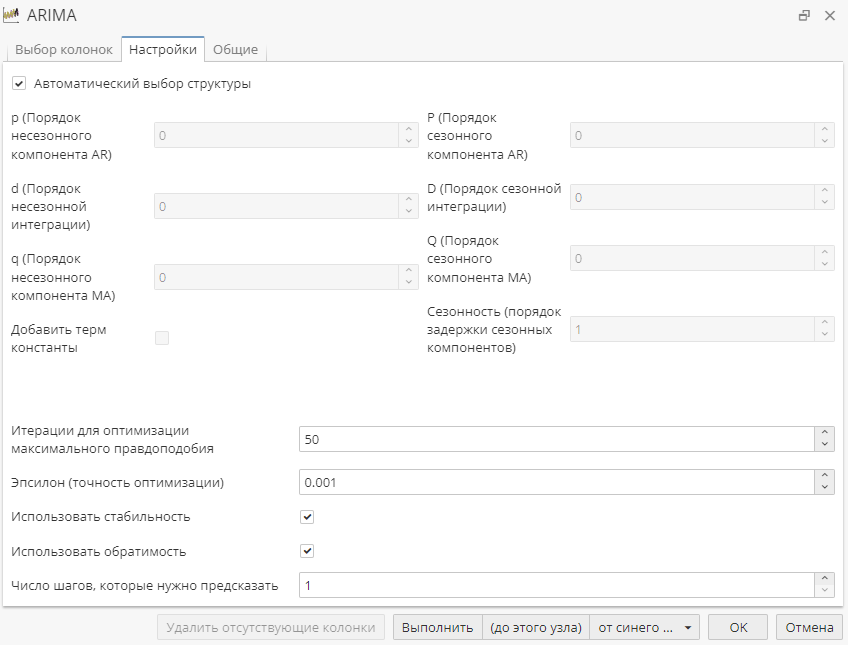
The p, d, q, P, D, Q и Сезонность - это стандартные параметры моделей ARIMA:
-
Параметр AR модели ARIMA указывает на то, что изменяющаяся переменная подвергается регрессии на собственных значениях запаздывания:
-
p - Порядок несезонного компонента AR
-
P - Порядок сезонного компонента AR
-
-
Параметр I ("интегрированный") модели ARIMA указывает на то, что значения данных были заменены разницей между их значениями и предыдущими значениями (и этот процесс дифференцирования может быть выполнен более одного раза):
-
d - Порядок несезонной интеграции
-
D - Порядок сезонной интеграции
-
-
Параметр MA модели ARIMA указывает на то, что ошибка регрессии фактически является линейной комбинацией условий ошибки, значения которых произошли одновременно и в разное время в прошлом:
-
q - Порядок несезонного компонента MA
-
Q - Порядок сезонного компонента MA
-
-
Сезонность - это порядок задержки сезонных компонентов.
Цель каждого из этих параметров - достичь максимального соответствия данным.
Для удобства пользователя по умолчанию структура модели выбрана автоматически: опция Автоматический выбор структуры включена.
Другие опции включают:
-
Добавить терм константы - позволяет добавить константу в формулу; также называется безусловным средним. Модель работает не отностительно нулевого значения, а относительно некоторого среднего значения, заданного константой;
-
Итерации для оптимизации максимального правдоподобия - число итерации максимизации функции правдоподобия;
-
Эпсилон (точность оптимизации) - точность оптимизации, при достижении которой завершаются Итерации для оптимизации максимального правдоподобия;
-
Использовать стабильность - гарантирует что модель будет устойчивой. "Стабильные" параметры модели ARIMA отображаются на \(R^{n}\) таким образом, что в случае обратного отображения в "изначальное" пространство параметров корни характеристического полинома модели всегда будут внутри единичной окружности на z-плоскости, т.е. модель всегда будет устойчивой. При этом максимизация правдоподобия производится в этом "устойчивом" пространстве методами безусловной оптимизации, а "настоящие" параметры модели получают обратным отображением в оригинальное пространство параметров.
-
Использовать обратимость - гарантирует, что модель будет обратимой. Данная процедура аналогично процедуре, используемой в опции Использовать стабильность, но в данном случае процедура используется не для полюсов, а для нулей системы;
-
Число шагов, которые нужно предсказать - число шагов/выборки вперед (в будущее), которые нужно предсказать.